A szögfüggvényeket a trigonometriában használják. A köztudatban csak szinusz, koszinusz, tangens néven ismerik, és nehéznek tartják.
Tartalomjegyzék
Függvények
Fajtái
Ábrázolása
Függvények és grafikonok
Szögfüggvények
Ábrázolása
Derékszögű háromszögben
Definíció az egységsugarú kör, illetve egységvektor segítségével
Végtelen sorral
Differenciálegyenletekkel
Komplex szögfüggvények
Függvények
Függvény olyan szabály, amely az értékek egy bizonyos halmazához egy másik értékhalmazt rendel. Az első halmaz minden eleméhez a második halmazból pontosan egy elemet rendel hozzá. Az olyan szabályok mint a „duplázd”, „emeld négyzetre” vagy „adj hozzá 1-et”, mind függvények. Egy függvényt általában „f” betűvel (vagy bármilyen más kisbetűvel) jelölünk.
A függvény másik elnevezése hozzárendelés. A hozzárendelés jelölése más. Pl. „f(x)=2x” függvény hozzárendeléses jelölése: „f:x→2x”.
A függvény részei/értékei
–Helyettesítési érték (függvényérték)
Az az érték, amelyet a függvény az x helyen felvesz. Jele: f(x).
A függvényérték halmazát az „f” függvény értékkészletének hívjuk, ez a képhalmaz részhalmaza.
–Értelmezési tartomány
Azoknak a számoknak a halmaza, amelyekhez a függvény hozzárendel értéket.
–Képhalmaz
Olyan halmaz, amelynek az értékkészlet részhalmaza. Általában valós számok halmaza.
A függvények fajtái
Összetett függvény
Kettő vagy több függvény kombinációja, egymás utáni elvégzése.
Jele: f [g(x)].
Azt jelenti, hogy előbb a g függvény helyettesítési értékét kell kiszámolni az „x” helyen, azután az így kapott értéket kell behelyettesíteni az „f” függvény hozzárendelési szabályába.
Inverz függvény
Egy művelet vagy műveletek sorozata, amely megfordítja a függvényt. Általában f-1(x)-szel jelöljük.
A függvények ábrázolása
Sokféleképpen jeleníthetjük meg a függvényeket pl. halmazábra, számegyenes, folyamatábra, grafikus.
Halmazábra
Halmazábra
Az értelmezési tartomány minden egyes elemét összekötjük a képhalmaz 1-1 elemével.
Számegyenesek
Az értelmezési tartomány minden egyes elemét összekötjük a képhalmaz 1-1 elemével.
Folyamatábra
A függvényérték kiszámításának műveleti sorrendjében történik.
Függvények és grafikonok
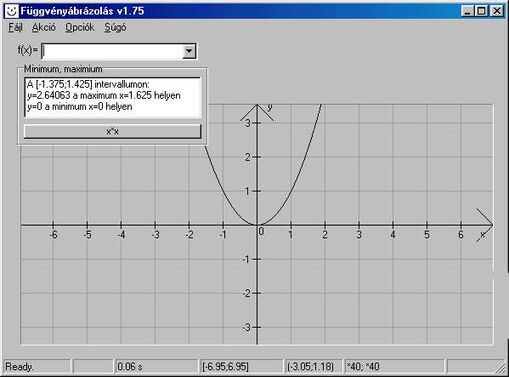
A függvényeket grafikonokkal is ábrázolhatjuk. Az értelmezési tartomány az „x” tengelyen (vízszintes), a helyettesítési értékek pedig az „y” tengelyen (függőleges) találhatók.
Minden függvény ábrázolható grafikonnal, ami csak rá jellemző.
A grafikonokról különféle információkat olvashatunk le.
Ennek képlete a következő:
Grafikon alatti terület= „x” tengelyen mért távolság x „y” tengelyen mért távolság. (x=szorozva)
Függvények ábrázolása
A grafikonok fajtái a következők:
– lineáris függvény
Az összes f(x)=mx+b alakú függvény (ahol „m” nem lehet 0).
– másodfokú függvény
Az összes f(x)=ax2+bx+c alakú függvény (ahol „a”, „b”, „c” és „d” konstansok és „a” nem lehet 0).
– harmadfokú függvény
Az összes f(x)=ax3+bx2+cx+d alakú függvény (ahol „a”, „b”, „c” és „d” konstansok és „a” nem lehet 0.
– exponenciális függvény
Az összes f(x)=ax alakú függvény (ahol „a” konstans).
– reciprokfüggvény
– racionális törtfüggvény
– körfüggvény
– trigonometrikus függvény
Az f(x)=sin x, f(x)= cos x, és f(x)=tg x függvények.
Szögfüggvények
Szögfüggvények
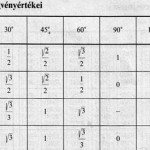
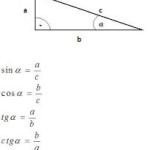
A szögfüggvényeknek 3 fajtája van: szinusz, koszinusz, tangens.
Ezek arra valók, hogy a háromszög szögei és oldalai közötti összefüggéseket mutassák meg a trigonometriában. (erről bővebben olvashatnak a Háromszög szócikkben)
Derékszögű háromszög részei
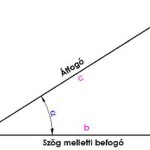
Szinuszt akkor használjuk, ha ismerjük, vagy ismernünk kéne a szöggel szemközti befogót, vagy az átfogót.
Koszinuszt akkor használjuk, ha ismerjük vagy ismernünk kéne a szög melletti befogót, vagy az átfogót.
Tangenst akkor használjuk, ha ismerjük, vagy ismernünk kéne a szög melletti, vagy a szöggel szemközti befogót.
A szögfüggvények ábrázolása
1. rész
2. rész
3. rész
4. rész
Definíció a derékszögű háromszögben
Derékszögű háromszög tételei
Definíció az egységsugarú kör, illetve az egységvektor segítségével
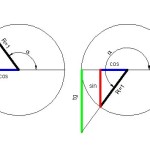
A szögfüggvények az egységsugarú kör segítségével is meghatározhatók. Ezáltal a szögfüggvényeket az összes pozitív és negatív szögre kiterjeszthetjük. Az egységsugarú Kör jól látható segítséget nyújt a szögfüggvényeket értelmező összes derékszögű háromszög megmutatására.
Egységsugarú körrel
Ennek módja a következő:
A kör középpontjában felveszünk egy derékszögű koordináta-rendszert. Rajzoljunk fel egy derékszögű háromszöget, amelynek egyik befogója az x tengelyre esik, egyik csúcspontja a középpontban van. Átfogója az egységsugarú kör sugara, a középpontban lévő szög α. Az átfogó kör kerületére eső pontjának x koordinátája cos α, y koordinátája pedig sin α lesz. Képlete így írható le: sin α = y/1 és cos α = x/1.
Definíció végtelen sorral
Ha geometriát és a határérték tulajdonságait használjuk, akkor kijön az, hogy a szinusz függvény deriváltja a koszinusz függvény és a koszinusz függvény deriváltja a mínusz szinusz.
A végtelen sorok elméletét a valós számok rendszere alapján lehet levezetni mindentől függetlenül. Sokszor csak a szinusz és a koszinusz van megadva, így a többi szögfüggvényt hányadosokként, vagy reciprokként határozzák meg.
Definíció differenciálegyenletekkel
Komplex szögfüggvények
A szinusz és a koszinusz hatványsoruk, az Euler-formula, vagy differenciálegyenlettel kiterjeszthető a teljes számsíkra. Ezzel a kiterjesztéssel nem lesznek újabb nullhelyek, valamint ugyanúgy teljesülnek a függvényegyenletek, de a korlátosság elvész.
A többi szögfüggvény kiterjesztését a szinusz és a koszinusz segítségével végzik; ezzel a függvényegyenletek továbbra is megmaradnak, és nem keletkeznek újabb végek, vagy zérushelyek.
Egy szó, mint száz: a matematika bonyolult tudomány. Reméljük, hasznosak voltak ezek az információk.
5 kérdés, 5 válasz
1. Mit nevezünk függvénynek? – Olyan szabály, amely értékhalmazhoz értékhalmazt rendel.
2. Hogyan jeleníthetők meg a függvények? – Halmazábrával, folyamatábrával, grafikonnal.
3. Milyen függvények vannak? – Többféle van, pl. összetett, inverz, lineáris, másodfokú, stb..
4. Milyen függvényekkel írhatók le a háromszög szögei és oldalai közötti összefüggések? – Szinusz, koszinusz, tangens szögfüggvénnyel.
5. A matematika melyik ága foglalkozik a függvényekkel? – A trigonometria.
Képforrás:
Kiemelt kép: home.sch.bme,
halmazok, matekotthon, Szögfüggvények
Forrás:
Matematika képes szótár Novum Kiadó 2004.
math.bme, Nevezetesfv, Matematika_7-6_A_fuggvenyek_abrazolasa, Szögfüggvények
Taylor-sor, trigonometria, szogfuggvenyek
A szerkesztő ajánlja, olvasd el te is!
Reméljük, tudtunk segíteni.
További szép napot kíván az fk-tudas szerkesztősége.
Tetszik a téma? Ossza meg ismerőseivel:
